Alla schackspelare är inte speciellt förtjusta i schackproblem - det har jag nog märkt! Trots det är det ändå hos schackspelare som en stor del av den tänkbara publiken finns. Ett normalt schackproblem kräver ju ganska mycket schackkunskap av betraktaren bara för att kunna begripas. För att inte tala om vad som krävs av lösaren.
Även om en tredragare går att lösa bara man vet schackreglerna, är det en stor fördel att ha en massa färdiga mattställningar i huvudet. Detta relativt höga krav på schackerfarenhet är ett hinder när det gäller att bredda intresset för vanliga schackproblem. Samtidigt finns det en stor mängd människor som gillar att lösa problem - allt från korsord till knepiga mattegåtor. För dessa människor kanske schackproblem av typen retrograd analys kan vara något.
Sherlock Holmes analyserar
Retrograd analys innebär i schacksammanhang att man försöker analysera en schackställning för att komma underfund med hur den kan ha uppkommit. Frågor som ställs kan gälla vem som måste vara vid draget, vad som var det senaste draget eller någon annan liknande faktor. Raymond Smullyan, professor i matematisk logik och filosofi, ger en utmärkt god och trevlig introduktion till ämnet i sin bok "Chess Mysteries of Sherlock Holmes" Här låter han den berömde detektiven gå omkring och analysera diverse schackställningar samtidigt som han undervisar sin gode vän doktor Watson i retroanalysens grunder. Han börjar med den lilla övningen i diagram 1.
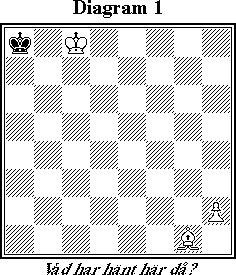
Vit spelar som vanligt uppåt i bild. Givet att svart drog senast - vad var hans senaste drag, och vad var vits drag innan dess?
Uppenbarligen måste svart senast ha flyttat kungen till a8, och lika klart måste denne ha kommit från a7. Sen blir det inte lika uppenbart. Hur kunde schacken av löparen på g1 uppstå? Löparen kan ju inte ha dragit längs diagonalen g1-a7, för då var det ju redan schack. Lika lite kan den ha kommit från h2, där det ju står en vit bonde. Hade vi inte vetat vilket håll vit spelade åt hade vi kunnat tro att löparen varit en promoverad bonde, men nu vet vi ju att vit spelar uppåt. Enda möjligheten är alltså att det var fråga om en avdragsschack. En avdragsschack med vad, kan man ju undra. Den vita kungen, som ser ut att vara den enda möjliga pjäsen, står ju långt ifrån den diagonalen. Nej, den enda möjligheten är att avdragsschacken utfördes av en pjäs, som senare har försvunnit från brädet. Och eftersom det enda svart har gjort har varit att dra kung a7-a8, måste den vita pjäsen ha slagits där. Den enda pjäs som kan komma från den aktuella diagonalen till a8 i ett drag är en springare och de två senaste dragen är alltså 1. Sb6-a8+ Ka7xa8.
Det var väl egentligen inte svårt. (Det var nog besvärligare för mig att skriva ned än det var för er att fatta.) Det illustrerar dock något jag vill minnas var Sherlock Holmes ledord, nämligen att:
"När man väl har uteslutit det omöjliga,
måste det som återstår vara det riktiga,
hur otroligt det än må låta."
Detta är det väsentliga att komma ihåg när man löser den här typen av problem. Sådana problem finns i alla svårighetsgrader, från ganska rättframma men ändå knepiga saker som ställningen i diagram 2, till ytterst knepiga och tillkrånglade saker som den i diagram 3.

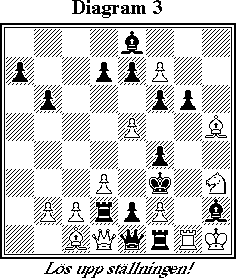
Diagram 2 har ni kanske sett förut. Den inleder Smullyans andra bok ("The Chess Mysteries of the Arabian Knights"), men har även förekommit på andra ställen i lite annan form. I Smullyans variant sägs det att den vite kungen står på brädet, men har gjort sig osynlig. Var står han? Lösningen kommer strax här nedanför, så vill ni grubbla själva så gör det nu!
Diagram 3 har ni knappast sett förut. Det är ett originalproblem av Nikita Plaksin publicerat i senaste numret av den svenska problemschacktidskriften Springaren. Uppmaningen här är helt enkelt "Lös upp ställningen". Det gäller alltså att försöka visa hur den här ihopknutna ställningen har uppstått. Enligt ledtråden i tidningen skall det hela klarna när man väl lyckats backa sådär en 14 (halv)drag.
Lösningen till diagram 2 är att vit kung måste stå på c3, och han måste i sitt senaste drag kommit från b3. Jag tänker inte gå in på detaljerna i beviset, men man kan snabbt övertyga sig om att enda möjligheten till vits löparschack är en avdragsschack av kungen, där kungen har flyttat ifrån b3. Lika väl är enda möjligheten till svarts föregående dubbelschack ett "en passant"-slag. De senaste dragen har alltså varit 1. - Ld5+ 2. c2-c4 b4xc3ep++ 3. Kxc3+. (Vit kan ju inte ha gått till a3 med kungen eftersom det då skulle ha stått kvar en svart bonde på c3 i diagramställningen.) Lösningen till problemet i diagram 3 kan jag tyvärr inte ge er, eftersom den inte har publicerats än. Man kan ju ana att vits senaste drag har varit Tg4-g1+. Men innan det, då?
Schack för logiker
Att som Smullyan gjort låta Sherlock Holmes agera problemlösare passar ganska bra eftersom retroproblem ofta liknar typiska deckargåtor. De finns i många former, även om typen "Vad var de senaste dragen?" kanske tillhör de vanligaste. (När man inte bara ska räkna ut de senaste dragen utan i stället visa hur hela partiet har förlöpt ser man det som den speciella klassen bevispartier, något som jag skrivit om i ett par tidigare artiklar.)
Trots allt kanske den vanlige nötknäckaren tycker att det här är för torra problem. Han eller hon kanske mera gillar problem av typenä
Svart vann
(Hämtat från "Att knäcka nötter", När Var Hur-serien, 2.a upplagan 1966)
"De tre hästarna, som stod klara för start på kapplöpningsbanan, hette "Ptro", "Galopp" och "Gnägg", och utan att vi för den skull nämner dem i rätt ordningsföljd kan vi tala om, att de tre nämnda hästarna ägdes av Nisse, Sven och Janne. Dagen därpå kunde man läsa följande i ortstidningen:
"Gnägg" hade oturen att störta efter första hindret och bryta ett framben.
Jannes häst var en mörkbrun treåring.
"Galopp" hade i ett föregående lopp vunnit 7.500 kronor.
Det har framkommit, att Sven förlorade en betydande summa pengar, fast hästen höll på att vinna.
Hästen som vann loppet var svart.
Detta lopp var det första, som Nisses häst deltog i.
I tidningen stod naturligtvis också namnet på vinnande häst och dess ägare - men det kan ni lista ut på annat sätt."
För den nötknäckare som gillar denna typ av hemmalogik har Smullyan mycket att erbjuda. I de bägge böcker jag talat om här finns många problem som liknar exemplet ovan. Lösaren får diverse lösryckta fakta givna, där den aktuella ställningen kanske bara är en av flera pusselbitar. Det gäller sedan att med hjälp av dessa fakta lösa någon given gåta. Exemplet nedan är från "Arabian Knights", där Smullyan låter pjäserna ikläda sig roller och spela upp små scenarion som ska lösas. I dialogen nedan representerar kalifen Haroun Al Rashid den vite kungen och hans rådgivare visiren är vitfältslöparen, kungens löpare.
Mysteriet med de begravda tornen
(Fritt översatt från " The Chess Mysteries of the Arabian Knights", Raymond Smullyan, 1981)
"Var är mina bägge torn?", frågade Haroun sin visir en dag.
"Bägge är inte era", svarade den oförskämde visiren. "Ett av dem tillhör fru Haroun Al Rashid, vet ni väl."
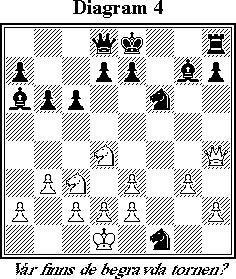
"Hur som helst", svarade Haroun, "jag undrar fortfarande vart de har tagit vägen."
"Om ni menar de två vita tornen, så blev bägge slagna under det här partiet och begravda på fläcken där de slogs."
"Men det är fruktansvärt!", sa Haroun. "Några av mina mest värdefulla skatter finns därinne - som det här manuskriptet, till exempel! Vi måste genast gräva upp dem!"
"Sextiofyra rutor innebär en väldig massa utgrävningar, ers majestät!"
"Vid Profetens skägg, människa, minns du inte var de blev slagna?"
"Nej", svarade visiren. "Ingen minns det. Allt som har bokförts är att de blev slagna på samma rad."
"Inte mycket hjälp", svarade den uppretade kalifen.
"Nej", sa visiren.
"Nåväl, gör något!", vrålade kalifen.
Vad kunde han göra? Han hörde sig för med krönikeskrivaren, som fast han inte visste var de vita tornen var begravda, dock mindes att det svarta damtornet hade slagits av en bonde.
"Den här informationen kan komma till nytta", sa Haroun. "Jag minns också att du inte deltog i det här partiet. Har jag inte rätt?", frågade han visiren.
"Korrekt, ers majestät, jag deltog inte. Jag blev sjuk på stridens första dag och måste avlägsnas från fältet. Jag blev, som man säger, en löpare som gavs i förgåva."
"Sjuk eller lat?", skrek Haroun.
"Sjuk", svarade visiren.
"Nåja, låt oss inte gräla. Mycket större saker står på spel. Jag måste finna mina torn!"
"Ni menar de vita tornen", rättade visiren.
"Åh, lägg av, människa, kan du inte vara tyst! Låt mig tänka: De bägge tornen slogs på samma rad, svarts damtorn slog av en bonde, och vits kungslöpare gavs i förgåva. Det räcker inte - problemet är olösligt!"
Precis då nåddes de av nyheten att svart var på väg att rockera. "Prisad vare Allah", utropade kalifen, "mysteriet är löst! Nu kan jag finna mina skatter!"
Var finns de begravda tornen?
Elementärt, min käre Watson
Lösningen till problemet med de begravda tornen går ungefär så här:
- Svarts saknade torn har slagits av en bonde. Vits bönder har inte hunnit så långt, och det enda slaget har uppenbarligen skett på e3. Tornet måste alltså ha slagits här.
- Svart kan fortfarande rockera, vilket innebär att svarts kung aldrig har flyttat. Svarts torn kan alltså inte ha kommit ut den vägen. Den enda möjligheten då är att svarts b- och c-bönder har slagit i kors för att släppa ut tornet.
- Vit saknar, förutom vitfältslöparen som gavs i förgåva, även svartfältslöparen och bägge tornen. Två av dessa tre pjäser måste ha slagits på b6 och c6. Men innan det svarta tornet slogs på e3 kunde inget av de vita tornen komma ut! Alltså måste det första som hänt varit att vits svartfältslöpare slagits på b6.
- Tyvärr räcker inte detta för att a8-tornet skall komma ut. Svarts vitfältslöpare måste också bort. Och här kommer kanske en överraskning - eftersom ingen vit pjäs ännu kan offras på c6 för att låta b7-bonden slå och släppa ut löparen, måste den ha slagits på sin ursprungsruta. Det betyder att löparen som nu står på a6 är en promoverad bonde.
- Hur har nu denna uppstått? Både svarts f- och g-bonde saknas och kan ha promoverat. Eftersom vit bara saknar ytterligare en pjäs (förutom de som vi redan tagit hänsyn till) kan svart inte ha slagit sig till h1. Promoveringen måste alltså ha skett på f1.
- Innan den promoverade löparen på f1 kunde lämna denna ruta måste g3 vara draget. Det betyder att när löparen lämnade f1 stod det redan bönder på d2, e3, g3 och h2. Alltså kan inte springaren på f1 ha kommit dit på normalt sätt utan måste även den vara en promoverad bonde. Den ena promoveringen skedde av f-bonden och den andra av g-bonden som någonstans på vägen slog vits återstående torn för att slå sig över till f-linjen.
- Nu har vi alltså alla fakta vi behöver. Vits svartfältslöpare slogs på b6, det ena vita tornet på c6 och det andra någonstans på f-linjen. Eftersom vi vet att de bägge tornen slogs på samma rad måste det andra tornet alltså ha slagits på f6.
Förresten, galopproblemet kan naturligtvis lösas ungefär så här:
En svart häst vann (5). Alltså kunde det inte vara Jannes häst (2). Svens häst vann inte heller (4). Alltså vann Nisses häst.
"Gnägg" kunde omöjligt vinna (1), varför Nisses häst måste heta "Galopp" eller "Ptro". "Galopp" hade tidigare vunnit 7.500 kronor (3), och då Nisses häst deltog för första gången (6), måste hans häst heta "Ptro".
Som sagt, för den som gillar den här typen av huvudbry och logiskt resonerande kan Smullyans böcker rekommenderas. Medan "Arabian Knights" kanske innehåller något mer originella problem är "Sherlock Holmes" nog den mer intressanta. Det är trevligt att följa dialogerna mellan Holmes och Watson under pågående analyser. Jag avslutar med ytterligare en ställning ur den sistnämnda boken.
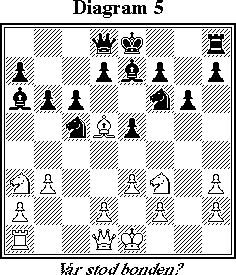
I denna ställning har en vit bonde just trillat ned på golvet och ingen av spelarna kommer ihåg var den stod. När Holmes får veta att ingen av kungarna ännu har flyttat kan han ställa tillbaka bonden.
Var stod den?
|



